전기자기학~인덕턴스, 전류가 흐르면 자속이 발생하는데, 이를 보충 해 주는 비례상수.

인덕턴스까지 왔다면, 앞으로 전기자기학에서는 전자계만 남았다.

여기까지 따라오느라 수고 많았다. 전자계란 무엇이냐? 먼저 실수와 허수를 생각하면 된다. 일반 전류와 변위전류와의 관계에서 유전체의 손실률에 대해... 아... 오늘은 인덕턴스지...

 

인덕턴스는 앞선 part와는 달리 몇 개 외워야(?)하는 공식이 있을 뿐 이것만 외무면 정말 쉬운 part다. 틀리면 부끄러운 줄 알아야...

 

우선 인덕턴스란 무엇이냐?

8장 전자 유도와 인덕턴스 - 2 : 네이버 블로그 (naver.com)

8장 전자 유도와 인덕턴스 - 2

여기에서 엄청 설명이 잘 되 있으니 먼저 참고하길 바란다.

 

다만, 아는 사람 눈에는 정말 쉽게 정리가 잘 되어 있는데, 모르는 분들에게는 복잡 해 보이니 오늘도 쉽게 쉽게 접근 해 보도록 하자.

 

자기인덕턴스 별거 없다. LI=NΦ만 기억하면 된다.

제목과 같이 L 인덕턴스는 전류와 자속과의 관계를 보충 해 주는 비례상수의 역할을 한다. 그래서 식으로 나타내면,

이렇게 나타내는데 이것만 봐도 오늘 수업은 끝이다.

앞서 언급했다 싶이 환상솔레노이드의 자계의 세기(H)는

이거임으로 저렇게 환상솔레노이드 자기인덕턴스 값으로

이 값을 도출 할 수 있다. 그렇다면, 무한 솔레노이드는 어떻게 할까? 무한솔레노이드 자계의 공식은 H=NI다. 그러면 결국 우리는 저식에서 길이인 L자를 제외한

이 값이 무한솔레노이드의 자기인덕턴스 공식임을 짐작 할 수 있다.

그럼 이로서 인덕턴스는 part는 다 끝났다.

 

나머지 합성인덕턴스, 동축인덕턴스, 평행도선 인덕턴스도 책에 나온대로 돌파하면 된다.

 

자, 이제 문제를 풀어볼까?

어 병렬이네... 그런다면, L1L2/L1+L2라는 형태는 분명히 띌거고... 점이 동일하니 가동접속이고... 그럼 답은 2번이네.

이렇게 쉬워??? 그런데 님아... 님 설명 해 준 것으로는 못 풀겠는데요...

그니까... 나머지는 외워야 한다.

이 형태는 합성인덕턴스의 병렬 형태로 코일의 합성인덕턴스가 동일하면(가동접속),

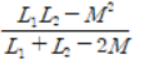
이 모양이고, 차동접속(다르면)이면,

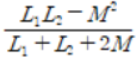
이 모양이다. 즉 2m 앞에 +, -만 바뀌니 걍 외우면 된다.

 

일반적으로 인덕턴스는 저항과 같이 결합하면 된다.

다만, 상호인덕턴스가 발생 시 위의 식을 적용한다.

 

자, 다음문제

 

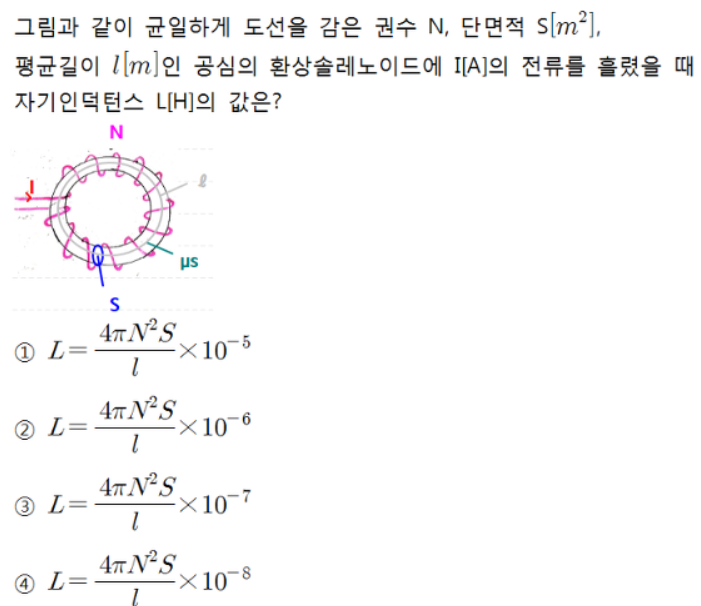
문제 말고 답을 봐라... 환상이지... 그럼

이런 형태 일 것이고, 투자율이 얼마더라... 아! 십의 마이너스 칠승! 그럼 3번이네.

 

뭐, 이렇게 인덕턴스는 무리없이 다 풀 수 있다.

 

오늘은 산타클로스가 오는 날이다.

산타는 있으니 다들 일찍 자라.

 

솔직히 이 part는 이해 할까 싶다가다도 어느새 외워져 버려서... 설명 할 내용이 그닥 없다.