회로이론이라 하여, 긴장을 했었는데, 별거 없었다.
그래서 기본에서 유도를 거쳐 지금은 중첩의 정리 등을 상대하고 있는데, 이를 굳이 설명 해야 할까 싶어 한동안 쓰지 않았다. 보면 다 안다.
중첩의 정리란 일부다처제를 의미하는 것이 아니라, 전압원이나 전류원이 여러개 있을 경우, 전압원은 단락 시키고, 전류원은 개방 시켜 각 경우의 전류를 합쳐 회로를 정리 한 것이다.

그렇다. 지금부터 설명 할 것들은 복잡한 회로도를 간단하게 정리하여 보기 좋게 만든 뒤 맛있게 냠냠 하는 것이다.
어찌보면, 원리는 간단하다. 다만, 많은 경우의 수가 있어, 문제를 풀면서 체득하는 것이 중요하다. but 어느정도 수준이 되면, 직렬의 전압 분배의 법칙, 병렬의 전류 분배의 법칙만으로도 쉽게 정리 할 수 있다.
참고로 키르히호프의 법칙이 생각나는데, 이것도 간단하다.
키르히호프의 제 1법칙, 들어간 전류와 나간 전류는 같다. 즉, 전류의 대수의 합은 0이다.
키르히호프의 제 2법칙, 기전력의 합은 내부저항과 전압을 곱한 전압강하와 같다.
즉, 본디 전기는 소모 되는지라 발산의 정리에 의하여 사라지는 것이 맞지만, 폐회로가 성립 된다면, 그 양을 유지한다는 의미다. 어찌보면 등가교환의 법칙에 비유 할 수 있는데, 그래서 이 part에서도 등회로 법칙으로 위의 정리나 원리를 사용하는 것이다.
테브낭의 정리란 노빡구의 정리와 쌍대를 이루고 있는 법칙으로서, 동시에 전압원은 단락시키고, 전류원은 개방하여 회로도를 쉽게 보게 하는 정리법이다.
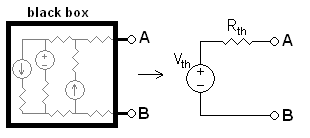
중첩의 정리든 테브낭의 정리든 편한 것을 사용하면 된다. 테브낭의 경우 전압은 개방된 a, b 양단의 전압을 구하면 되는데, 주로 직렬 전압의 분배를 많이 이용하고, 임피던스(저항)의 경우 반대로 보아, 저항을 합치면 된다. 주로 직류 + 병렬의 저항 모양으로 계산 된다.
밀만의 정리란 같은 주파수의 전압원이 병렬로 구속 되어 있을 때, 이를 v=ir 형태로 정리하여, 전압값을 구하는 식이다.
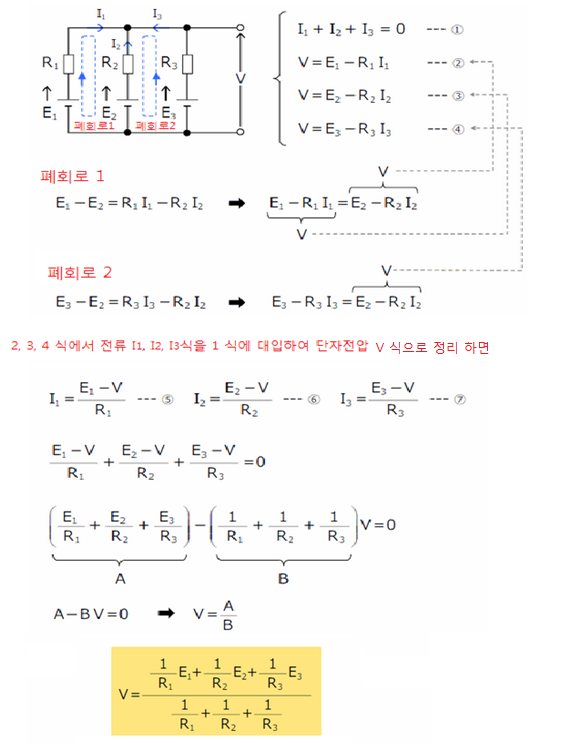
와... 복잡하게 설명 해 놓았다. 걍 V=IR, I=V/R, Y=1/R만 알면, 이를 정리하면 되는데... 이러니, 사람들이 산은 오르지도 않고 뫼만 높다하는거지... 졸라 쉬운 내용을 이리 귀찮게 설명하고 있으니...
가역의 정리란 등가교환의 법칙의 일종이다. 회로를 중심으로 하여 양쪽 전력이 일치한다는 것이다.

이 것을 보니, 휘스톤브리지가 생각난다.
사실, 앞서 역률이라든지, 피타고라스의 정리라든지 그런 내용들이 나오는데, 초기에 다 다룬 내용이라 걍 산책한다 생각하고 보면 된다. 이 회로이론의 강점(?)은 문제는 쉬운데, 계산기를 많이 두드려야 한다는 것이다. 그러니, 문제 풀다 계산기 두드리기 싫으면, 계산식만 적고 일치하는지 보고, 넘어가자. 지친다. 시간도 없고.
자 문제 함 풀어보자.
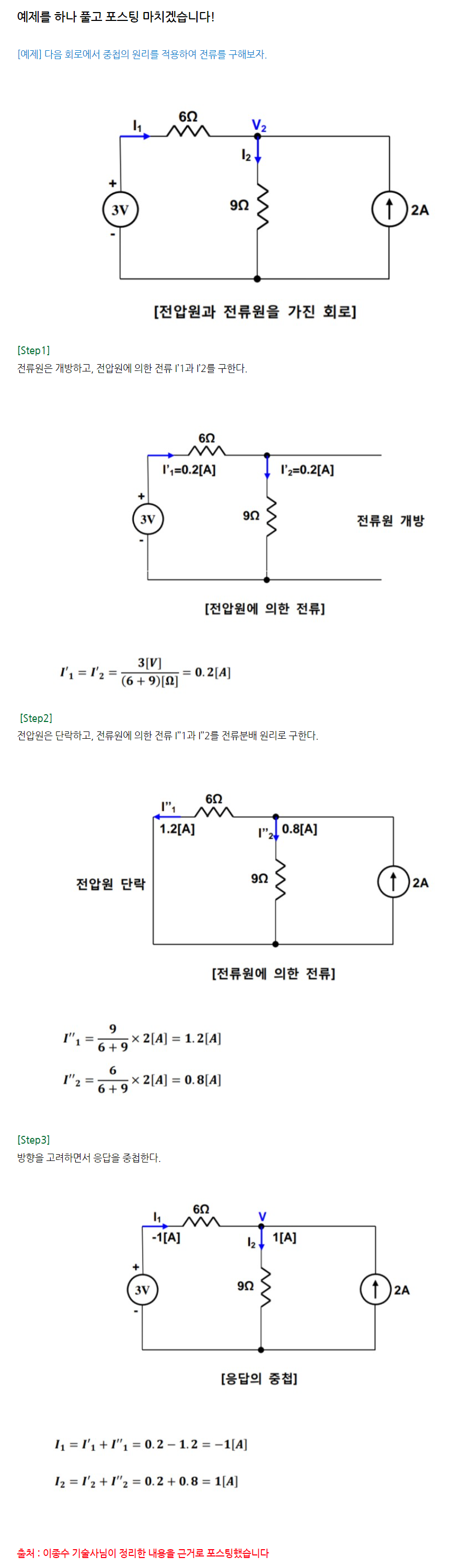
이렇게 설명이 잘 되 있으면... 내가 할일이 없잖니....

테브낭도 뭐 이렇게 풀면... 된다...
이렇게 쉬운 것을 어떻게 하면 어렵게 설명 할 수가 있지?????

#태양광 상담은(010-2668-3897)...




















RECENT COMMENT